OpenVDB  9.0.1
AX

AX Language Documentation

Welcome to the AX Language documentation. These docs provide detailed information on the AX language including syntax, data types, available functionality (including OpenVDB specific methods) execution structure and control flow. See the OpenVDB AX documentation for the C++ developer documentation.
Note
Some sections of this document are still to be completed. Please get in touch should you have any questions!

Contents

Introduction

AX is a fast and portable JIT compiled expression language, designed for writing volume and point kernels represented as OpenVDB grids. It was originally developed by the RNDFX team at DNEG to provide a more consistent way for artists to be able to interface with OpenVDB data across a variety of in house and external digital content creation software, whilst retaining the performance achievable by custom C++ operators.
The language is predominately inspired by SideFX's VEX language which itself takes elements from C, C++ and the Renderman Shading Language. The design of AX uses concepts from these languages and refrains from deviating from their syntax too significantly. Specifically, it does not aim to change what are already well established and heavily used language syntaxes within the Visual Effects industry; on the contrary, AX aims to provide an interface to which a user with previous or little programming experience can easily transition to. However, it does introduce new concepts where the creators deemed necessary to provide the best and most representative syntax relating to the design for OpenVDB volume and point modification.

AX Programs

AX programs represent a set of statements which read and write to geometry, with each program designed in such a way that it can be executed in a highly parallelized framework to access and update individual geometric components. For example, consider a mesh with point, vertex and primitive attributes. AX programs are designed to run independently across "elements" of input geometry and process "attributes" from a particular element. In this case, the element level would correlate to either points, vertexes or primitives, and a single element would be a unique instance of one of these. These programs are at their most efficient writing to the currently processing element, however do provide varying levels of access to the geometry as a whole.
Note that native AX only supports the modification of OpenVDB data. Currently, that means that native AX programs can be written and built for execution over OpenVDB Points or OpenVDB Volumes. For any given AX program, the execution context (what it's processing) may change what functionality is available and, more importantly, the behaviour of reading/writing from attributes. See the OpenVDB Execution Context for details.
Whilst powerful, AX is not a catch all replacement for all types of VDB operations. Some of this is related to its infancy i.e. missing native support for some useful functions, the foundations of which may be supported by AX but have not yet been exposed. However there may be certain paradigms which AX is better tailored to support than others. Grid reductions, for example, typically require the passing of a state between programs; a design pattern which AX is less equipped to handle. AX kernels can be abstractly thought of as a "foreach()" function (see A Program Example) and whilst there are ways to achieve reductions, it is an example which would be better suited to a custom C++ implementation.
For details of extending AX for custom geometry, see the OpenVDB AX developer documentation. Note that custom geometry support requires C++ extension.

A Program Example

Before getting into the technical depths of the language, it's a good idea to observe a small but complete AX program which could be compiled and executed. To begin with, here is a very simple example of a program that reads and writes to a particular attribute:
// read a floating point attribute from the value of "myattribute"
float temp = float@myattribute;
// if the value is less than 0, clamp it to 0
if (temp < 0.0f) float@myattribute = 0.0f;
Note that there is no other required logic here to make this a compatible program i.e. feeding this code to the vdb_ax command line binary will compile and execute over provided OpenVDB files.
The following explains the above example in relation to OpenVDB data; OpenVDB points and OpenVDB volumes. The example demonstrates reading from a value on some input, either a point attribute or a voxel value, and storing the result in a local variable. Importantly, the attribute being accessed has the name myattribute and the type float. The first statement:
float temp = float@myattribute;
Invokes a read from this attribute (see Attribute Access), retrieving the value from the geometry and storing it in the variable temp to be used in the AX program. The second statement:
if (temp > 0.0f) float@myattribute = 0.0f;
Performs a comparison of this value with 0.0f and, if the value is greater than 0.0f, performs a write to the geometry in the form of float@myattribute = 0.0f; which sets the value of this attribute on the geometry to 0.0f.
For OpenVDB Points, this kernel is run over every point in an OpenVDB Points Grid. In simple pseudo code:
1 foreach(point in pointgrid)
2  run_ax_kernel(point)
3 done()
Where pointgrid is a single Point Data Grid. For OpenVDB volumes the kernel is run over each voxel in a provided grid:
1 foreach(grid in grids)
2  foreach(voxel IN grid)
3  run_ax_kernel(voxel)
4  done()
5 done()
Where grids can comprise of any number of OpenVDB volumes. In this program, only a floating point grid with the name myattribute will be updated. Each voxel in this grid will have it's value compared in the same way as the points example given above.

OpenVDB Execution Context

AX programs are designed to run over different types of grids, specifically OpenVDB points and OpenVDB volumes, the latter of which is the set of all default supported mathematic volume types in OpenVDB. Programs must be compiled separately for points and volumes, or twice to support both (see the vdb_ax binary). This is known as compiling for a target Execution Context. There are two main considerations to make when switching between execution contexts:
  • Certain functions may not be available under a given context. Some natively supported functions are designed to interface directly with geometry attributes, and a further subset of these are tailored specifically for point attributes or voxel values, not both.
  • Whilst the AX grammar does not change syntactically, attribute accesses may be affected. This is due to the fundamental differences of executing over different types of VDBs/geometry.
Execution over Points
AX kernels compiled for OpenVDB Points run individually on each point in every active voxel in a points VDB. Attributes that have been accessed in the program are provided such that the program has access to all data available on the currently processing point. Multiple OpenVDB Point grids can be processed by the same AX program, but only a single OpenVDB Points grid can be processed at a time. The default behaviour for AX point programs is to process every point which exists in active OpenVDB voxels.
Execution over Volumes
AX kernels for OpenVDB volumes run individually on every active voxel of VDBs which are written to (whilst retaining access to all available VDBs). Volumes can be thought of as only holding a single "attribute". Whilst points hold all attributes within a single VDB points grid (and values for all attributes are are defined for all points in that grid), multiple volume attributes require multiple VDB volumes to be accessed. The location of this access is the world space position of each voxel. Assignment operations determine which volumes will be executed over.
See the syntax section on accessing attribute for more information.

Data Types

AX supports a rich variety of native types to be able to maximise the efficiency of arithmetic operations and facilitate accessing underlying geometry. As AX is designed for OpenVDB, native AX types aim to provide direct access to all supported OpenVDB data types. You may find, however, that some AX types do not exist as OpenVDB volume/point types or refuse to be serialized in some installations of OpenVDB. The table below lists all available types in AX, the exposed attribute access syntax and whether or not the attribute syntax is valid for both point and volume execution contexts. Developers installing OpenVDB and OpenVDB AX may wish to read the type registry documentation which explains how to enable missing types from OpenVDB.
CategoryTypeDefinitionAttribute SyntaxPointsVoxels
Scalars bool Boolean value, true or falsebool@ Yes Yes
int16*16-bit signed integer valueint16@Yes No
int3232-bit signed integer valueint32@, int@, i@Yes Yes
intAlias for integer type (typically int32)
int6464-bit signed integer valueint64@Yes Yes
float32-bit floating point valuefloat@ f@ @Yes Yes
double64-bit floating point valuedouble@Yes Yes
Vectors vec2i 2-element vector of integer values vec2i@ No No
vec2f2-element vector of float values vec2f@NoNo
vec2d2-element vector of double values vec2d@NoNo
vec3i3-element vector of integer valuesvec3i@Yes Yes
vec3f3-element vector of float values vec3f@ v@Yes Yes
vec3d3-element vector of double values vec3d@Yes Yes
vec4i4-element vector of integer valuesvec4i@NoNo
vec4f4-element vector of float values vec4f@NoNo
vec4d4-element vector of double values vec4d@NoNo
Matrices mat3f 3x3-matrix of float values mat3f@ Yes No
mat3d3x3-matrix of double valuesmat3d@Yes No
mat4f4x4-matrix of float values mat4f@Yes No
mat4d4x4-matrix of double valuesmat4d@Yes No
Strings string A string of characters string@ Yes Yes
  • Note* - There is no support for int16 local variables or integer literals.

Scalars

AX Supports boolean, integer and floating point scalar types. int and int32 represent 32-bit integer values and int64 represents a 64-bit value. float and double represent 32-bit and 64-bit floating point values respectively. All scalars, excluding bools, are signed; there are no other unsigned scalar types in AX.
Integer Overflow and Floating Point Truncation
Scalars may be cast from one type to another, either explicitly using the cast operator or implicitly during assignments or binary arthimetic operations (in which case the order of type precedence is observed). Data can be truncated (converting floats to integrals) or overflow (conversions from integers of larger bit widths to integers of smaller bit widths) depending on the source and target types. See the below examples:
This example demonstrates floating point truncation in AX.
float a = 1.1f;
int b = 5.5f; // implict conversion from literal 5.5f. "b" is set to 5
b = a; // implicit conversion from float "a". "b" is set to 1
This example demonstrates integer overflow in AX.
int64 a = 2147483648l; // one more than can be held in an int (note the last letter "l")
int b = a; // implicit conversion. "b" is set to -2147483648
Infinite and NaN values
Floating point values have two additional intrinsic states; inf and nan. These states can occur during invalid floating point arithmetic. AX performs no checks on arithmetic to catch these values. A typical example of both inf and nan values are division by zero expressions:
float a = 1.0f/0.0f;
print(a); // prints "inf"
float a = 0.0f/0.0f;
print(a); // prints some version of "nan"
Generally these values are not desired and can cause problems as they propagate throughout your program.

Vectors / Matrices

All vector and matrix types in AX are implemented as flat arrays of a given size, with all elements stored contiguously in memory. Both container types are represented by specific tokens which tell AX functions and operators how to handle various arithmetic.
Vectors
There is currently support for vectors of sizes 2, 3 and 4 elements. The suffix letter on the vector types denotes the contained elements precision, with the number corresponding to the vector size. For example, vec2i denotes a vector of two 32-bit integer elements. There are no native types for vectors with bool, int16 or int64 elements, so these are not supported.
Matrices
Matrices are stored in row major layout (lexographical access order) which matches the representation of a matrix in OpenVDB. Matrix support consists of float and double precision elements with dimensions either 3x3 or 4x4 (total size of 9 and 16 elements respectively). There are no integer or boolean matrix types. Similiar to vectors, the suffix letter on the type denotes the contained elements precision, with the number corresponding to the matrix dimension. A matrix of type mat3d therefor corresponds to a 3x3 matrix (9 elements) with double precision elements.
Element Access
As elements of all matrix and vector types are stored contiguously, they can be accessed by the [] operator. Vector elements can also be accessed by supported . operator components and matrix elements can be accessed with the [,] operator.
Initialization
Both matrices and vector declarations can be flat initialized from scalars or component initialized from containers of the same size (see assignments). However both types can also be represented as temporary containers without declarations using the {,} syntax.
A Note on Operators
Most binary operators only accept vectors of equal sizes as valid left and right operands - however there exists valid arithmetic for combinations of vectors/matrices with scalars and, importantly, multiplicative arithmetic for vectors with matrices, the latter performing matrix projections (transformations) on vector arguments.

Strings

Strings are an array of characters stored in a unique AX type which is incompatible with container accesses. As such, string support is currently fairly limited. Characters themselves (users may know this as a char type) have no frontend type, so a string type must be used for any number of characters (including the empty string). String literals are represented by enclosing any number of supported AX characters by quotes " ".

Implicit conversion / type precedence

All operators that perform on two or more types must internally run the operation at a single precision. When mixing different types (e.g. int + float) values may need to be converted to another type before the operation is performed. To allow for easier writing of expressions, AX will automatically detect these cases and convert values when necessary. This is known as implicit type conversion and the way in which the target operation type is chosen is known as type precedence.
When referring to type precedence, we are primarily refering to the conversion of one scalar type to another. For vectors, matrices and other containers, this refers to the conversion of their element type e.g. mat3f to mat3d. The conversion rules for more than the element type (e.g. int to mat4f) are governed by AX's assignment and operator rules, detailed in the Operators section of this documentation.
Type precedence only applies to the element type of the type in question. Containers (such as vectors or matrices) may change their element type precision (e.g. vec2i to vec2f). Each scalar type has a ranking which is compared, and the resulting highest rank is chosen as the target type for all values. These rankings are defined as follows:
  • If any element types are of type double, all other element types are converted to double
  • else, if any element types are of type float, all other element types are converted to float
  • else, if any element types are of type int64, all other element types are converted to int64
  • else, if any element types are of type int32, all other element types are converted to int32
  • else, all element types are bool
For example:
int a = 0;
float b = 0.0f;
// In the following, the arithmetic a + b chooses floating point precision as
// defined by the above type precedence rules (i.e. float(a) + b). The temporary
// value created by the arithmetic + will be at float precision. The subsequent
// assignment must then convert the final result back an integer, resulting in
// an expression equal to: a = int(float(a) + b);
a = a + b;
// This example shows arithmetic minus with a float scalar and vec4d. Minus is a
// supported operator of vec4d, however as the element types do not match
// (float vs double), implicit conversion must be observed. With the above rules,
// we can determine the following expression: c = double(b) + c. Note that
// as the result of "double(b) + c" is a vec4d and the target of the subsequent
// assignment ("c") is a vec4d, no further conversion needs to be performed.
vec4d c = 0.0; // double element type
c = b - c;
Strings are not included in this precedence as there are no supported arithmetic binary operations for strings with operand types other than string.

Operators

The below table lists all available operators supported by AX. Note that not all AX types support all operators and some operators have unique functionality depending on the operand types.
Operators
Binary Operators Unary Operators Other
Assignments Arithmetic Comparisons / Relational Logical Arithmetic Logical Increment / Decrement Container Access Other

a = b
a += b
a -= b
a *= b
a /= b
a %= b
a &= b
a |= b
a ^= b
a <<= b
a >>= b

a + b
a - b
a * b
a / b
a % b
a & b
a | b
a ^ b
a << b
a >> b

a == b
a != b
a < b
a > b
a <= b
a >= b

a && b
a || b

+a
-a
~a

!a

++a
--a
a++
a--

a[]
a[,]
a.b

a(...)
a, b
a ? b : c
{ a,b ... }

Binary Operators

Binary operators are the most common inbuilt operators for AX types. These operators take two inputs; a left hand side and a right hand side. There exists a number of valid combinations of AX types with different binary operators, as well as different implicit casting schemes depending on the binary operation being performed.

Assignments

Assignment operators are the only way to directly modify the value of local and external data (except for Functions which take references). The assignment operators have the following forms:
Operator NameOperator SyntaxReturns
Simple assignmentlhs = rhs Reference to lhs
Addition assignmentlhs += rhs Reference to lhs
Subtraction assignmentlhs -= rhs Reference to lhs
Multiplication assignmentlhs *= rhs Reference to lhs
Division assignmentlhs /= rhs Reference to lhs
Modulo assignmentlhs %= rhs Reference to lhs
Bitwise AND assignmentlhs &= rhs Reference to lhs
Bitwise OR assignmentlhs |= rhs Reference to lhs
Bitwise XOR assignmentlhs ^= rhs Reference to lhs
Bitwise shift left assignmentlhs <<= rhs Reference to lhs
Bitwise shift right assignmentlhs >>= rhs Reference to lhs
These can be further categorised into two types; direct assignment, which is comprised only of the simple assignment operator, and compound assignments, which is the set of all other assignment operators.
Direct Assignment
Direct assignments replace the contents of the lhs with a copy of the rhs:
lhs = rhs
The rhs side is not modified and the lhs is not read - only written to. If the rhs type does not match the lhs type, the rhs is first implicitly converted into a new temporary with the lhs type before being copied into the lhs. The following combination of AX type categories are supported for direct assignment (if an operation is not listed, it is not supported):
Left Operand TypeBinary Op(s)Right Operand TypeDescription
scalar= scalar On type mismatch, right hand side is copied and implicitly cast to the left hand side type.
vector = scalar Each element of the vector is set to the right hand side scalar. i.e.
a[0] = b; ... a[n-1] = b;
where n is the size of the vector. If the scalar type does not match element type of vector, the scalar is copied and implicitly cast to that type.
vector Component wise assignment i.e.
a[0] = b; ... a[n-1] = b;
where n is the size of the vector.
vec3f a = 0, b = 1;
a = b;
is equal to:
vec3f a = 0, b = 1;
for (int i = 0; i < 3; ++i) a[i] = b[i];
If the right hand side element type does not match the left hand side element type, each element of the right hand side is copied and implicitly cast to the target left hand side element type. Operand sizes must match.
matrix = scalar Diagonal matrix construction. Each diagonal component of the left hand side matrix is set to to the right hand side scalar. All other components are zero initialized i.e.
mat3f a;
int dim = 3, b = 1;
for (int i = 0; i < dim; ++i)
a[i] = (i % (dim+1) == 0) ? b : 0;
Where a is the matrix, dim is the dimension of the matrix (e.g. 3 for mat3f) and b is the scalar. If the scalar type does not match element type of matrix, the scalar is copied and implicitly cast to that type.
matrix Component wise assignment i.e.
a[0] = b[0]; ... a[n-1] = b[n-1];
where n is the total size of the matrix.
mat4f a = 0, b = 1;
a = b;
is equal to:
mat4f a = 0, b = 1;
for (int i = 0; i < 16; ++i) a[i] = b[i];
If the right hand side element type does not match the left hand side element type, each element of the right hand side is copied and implicitly cast to the target left hand side element type. Operand sizes must match.
string = string Replaces the contents of the left hand side string with a copy of the contents in the right hand side string.
float b;
vec3f c = 0.0f; // assign components of c (x/y/z) to an floating point literal of value 0.0f
int a = 1; // assign a from an integer literal of value 1
c = a; // assign components of c (x/y/z) to the result of float(a)
Compound Assignment
Compound assignments replace the the contents of the lhs with the result of a binary arithmetic operation of the lhs with the rhs:
lhs op rhs
Where op is one of :
+= -= *= /= %= &= |= ^= <<= >>=
The behaviour of a given compound assignment (for example a += b) is similar to replacing the compound assignment with a direct assignment followed by a binary expression with the same operands and given arithmetic token (i.e. a = a + b). However, compound assignments imporantly do not evaluate the lhs twice. This is important when assigning to an expression which is not an attribute or local value. The best example of this is assigning to a pre-crement operation:
int a = 1;
++a += 1; // equal to a = ++a + 1 which is equal to 3
The rhs side is not modified, however the lhs is both read from and written to. Note that the arithmetic operation may cast either lhs or rhs following the rules of AX's arithmetic type precedence. See the arithmetic operations section for more information on arithmetic type precedence and explanations on the above compound operators.
int a = 3;
a += a; // the same as a = a + a; a will be set to 6
float b = 0;
b -= a; // the same as b = b - float(a);
a *= b; // the same as a = float(a) * b; Note that although the target type is int, the binary op is performed at float precision
Assignment Chains
As assignments return a reference to the left hand side, all assignment operators can be chained. Note however that the return result will be at the type of the left hand side. For example:
Given
float a;
int b, c;
This
a = b = c = 4.5f;
is fundamentally the same as:
c = 4.5f; // c of type int. 4.5f will be floored (int(4.5)). c becomes 4
b = c; // b becomes 4
a = b; // a becomes float(4)
Importantly, a receives the result of any previous implicit casts to the right hand side of its binary assignment.

Arithmetic

Binary arithmetic operations compute the result of a arithmetic operand token on two inputs and returns the result. The inputs are not modified, however may be copied and implicitly cast to temporary values if the types do not match. All results are returned as new temporary values. If integral is explicitly stated, the operation is only valid on types which have an integer element type and will involve and implicit cast to integer types for floating point operands (the operation may be further restricted for container types). Binary arithmetic operations have the following forms:
Operator NameOperator SyntaxReturns
Additionlhs + rhs The sum of both operands
Subtractionlhs - rhs The first operand minus the second operand
Multiplicationlhs * rhs The product of both operands
Divisionlhs / rhs The first operand divided by the second operand
Modulolhs % rhs The floored modulo operator. See Multiplicative operands
Bitwise ANDlhs & rhs The integral bitwise AND result of each bit in the first operand applied to the bit at the same location in the second operand
Bitwise ORlhs | rhs The integral bitwise OR result of each bit in the first operand applied to the bit at the same location in the second operand
Bitwise XORlhs ^ rhs The integral bitwise XOR result of each bit in the first operand applied to the bit at the same location in the second operand
Bitwise shift leftlhs << rhs The integral bitwise left shift of the first operand by the second operand
Bitwise shift rightlhs >> rhs The integral bitwise right shift of the first operand by the second operand
Additive operands
Binary additive operations perform summations on the input arguments. They have the following forms:
lhs + rhs
lhs - rhs
After implicit conversion, the result of the binary operation with the arithmetic + (plus token) is the sum of the operands, and the result of the binary operation with the arithmetic - (minus token) token is the second operand subtracted from the first operand. The following combination of AX type categories are supported for additive operations (if an operation is not listed, it is not supported):
Left Operand TypeBinary Op(s)Right Operand TypeDescription
scalar+ -scalar Returns the result of the scalar addition or subtraction.
vector Performs per component binary operations (after implicit conversion) with the left hand side scalar to every element of the right hand side vector or matrix, returning a vector or matrix.
vec3f a = 2.0f;
int b = 1;
vec3f c = b + a;
is equal to:
vec3f a = 2.0f;
int b = 1;
vec3f c;
for (int i = 0; i < 3; ++i) c[i] = b + a[i];
matrix
vector + - scalar Same as scalar op vector
vector Performs per component binary operations (after implicit conversion), returning a new vector with each element holding the corresponding result. Operand sizes must match.
vec3f a = 2, b = 1;
vec3f c = a - b;
is equal to:
vec3f a = 2, b = 1;
vec3f c;
for (int i = 0; i < 3; ++i) c[i] = a[i] - b[i];
matrix + - scalar Same as scalar op matrix
matrix Performs per component binary operations (after implicit conversion), returning a new matrix with each element holding the corresponding result. Operand sizes must match.
mat4f a = 0, b = 1;
mat4f c = a - b;
is equal to:
mat4f a = 0, b = 1;
mat4f c;
for (int i = 0; i < 16; ++i) c[i] = a[i] - b[i];
string + string Performs string concatenation
Note
Floating point addition and subtraction is communicative (a + b = b + a) but is not necessarily associative. i.e. (a + b) + c is not necessarily equal to a + (b + c).
Examples of validity of additive operations:
int a = 0;
vec2f b = 1.0f;
vec2i c = 2;
mat4d d = 0.0;
c + a; // valid vec + scalar
c + d; // invalid vec + matrix
c - b; // valid vec - scalar
Multiplicative operands
The binary multiplicative operands have the following forms:
lhs * rhs
lhs / rhs
lhs % rhs
After implicit conversion, the result of the binary operation:
  • with the arithmetic * (asterisk token) is:
    • the product of the operands
    • OR performs matrix multiplication for vector and matrix types.
  • with the arithmetic / (forward slash token) is the first operand divided by the second operand.
  • with the arithmetic % (percentage token) is the floored modulo operations .i.e. the expression d % D returns the result D - d * floor(D/d). This is in contrast to truncated modulo operations D - d * (D/d) where the division is truncated.
Warning
Floored modulo has been chosen to provide better expected behaviour with signed dividends. In such cases the result will always be positive; in other words, the sign of the result is always taken from the divisor. This does however mean that the relationship properties between % and / differ when either d or D is negative. i.e.: (d/D)*D + (dD) != d
Note
The multiplicative operation * has important behaviour for vectors and matrix types.
The following combination of AX type categories are supported for multiplicative operations (if an operation is not listed, it is not supported):
Left Operand TypeBinary Op(s)Right Operand TypeDescription
scalar* / %scalar Returns the result of the scalar multiplication, division or remainder of the division respectively.
vector Performs per component binary operations (after implicit conversion) with the left hand side scalar to every element of the right hand side vector. The scalar is effectively treated as a vector of the same size as the right hand side type.
vec3f a = 2.0f;
int b = 1;
vec3f c = b * a;
is equal to:
vec3f a = 2.0f;
int b = 1;
vec3f c;
for (int i = 0; i < 3; ++i) c[i] = b * a[i];
*matrix Performs matrix multiplication after diagonal matrix construction from the left hand side scalar.
mat3f a = 1;
float b = 1;
mat3f c = a * b;
is equal to:
mat3f a = 1;
float b = 1;
mat3f tmp = b; // diagonal matrix
mat3f c = a * tmp;
vector * / % scalar Same as scalar op vector with the operands reversed (importantly for division and modulus)
vector Performs per component binary operations (after implicit conversion), returning a new vector with each element holding the corresponding result. Operand sizes must match.
vec3f a = 2, b = 1;
vec3f c = a * b;
is equal to:
vec3f a = 2, b = 1;
vec3f c;
for (int i = 0; i < 3; ++i) c[i] = a[i] * b[i];
*matrix Transforms the left hand side vector by the right hand side matrix using matrix multiplication. This is the same as calling the transform function. e.g:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
b = b * a;
is equal to:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
b = transform(b, a);
Typically, matrix multiplication requires arguments of the same dimension sizes - that is, a mat4 can only be applied to a vec4. However, it is often useful to be able to directly apply mat4 transformations to vec3 types, most often due to positions being represented as vec3. vec3 * mat4 multiplication is supported, where by the vec3 is extended with a 1 component and the resulting last last component is dropped from the return value:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
// b * a is equal to:
vec4f tmp;
tmp[0] = b[0];
tmp[1] = b[1];
tmp[2] = b[2];
tmp[3] = 1;
tmp = tmp * a;
b[0] = tmp[0];
b[1] = tmp[1];
b[2] = tmp[2];
Note: Valid operand sizes and return types match those of the transform function i.e:
  • vec3 * mat3 = vec3
  • vec3 * mat4 = vec3
  • vec4 * mat4 = vec4
matrix * scalar Same as scalar * matrix
vector Transforms the right hand side vector by the left hand side matrix using matrix multiplication. This is the same as calling the pretransform function. e.g:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
b = a * b;
is equal to:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
b = pretransform(a, b);
Typically, matrix multiplication requires arguments of the same dimension sizes - that is, a mat4 can only be applied to a vec4. However, it is often useful to be able to directly apply mat4 transformations to vec3 types, most often due to positions being represented as vec3. mat4 * vec3 multiplication is supported, where by the vec3 is extended with a 1 component and the resulting last last component is dropped from the return value:
mat4f a = identity4();
vec3f b = { 1, 2, 3 };
// a * b is equal to:
vec4f tmp;
tmp[0] = b[0];
tmp[1] = b[1];
tmp[2] = b[2];
tmp[3] = 1;
tmp = a * tmp;
b[0] = tmp[0];
b[1] = tmp[1];
b[2] = tmp[2];
Note: Valid operand sizes and return types match those of the pretransform function i.e:
  • mat3 * vec3 = vec3
  • mat4 * vec3 = vec3
  • mat4 * vec4 = vec4
matrix Performs matrix multiplication and returns the matrix product, which is matrix of matchign size and type. Operand sizes must match. e.g:
mat4f a = 1, b = 2;
mat4f c = a * b;
is equal to:
mat4f a = 1, b = 2;
mat4f c;
for(int i = 0; i < 4; ++i) {
for(int j = 0; j < 4; ++j) {
for(int k = 0; k < 4; ++k) {
c[i,j] += a[i,k] * b[k,j];
}
}
}
Note
Floating point multiplication is communicative (a * b = b * a) but is not necessarily associative. i.e. (a * b) * c is not necessarily equal to a * (b * c).
Bitwise operands
Binary bitwise operations have the following forms:
lhs & rhs
lhs | rhs
lhs ^ rhs
lhs << rhs
lhs >> rhs
These operations only run on integral operands. After implicit conversion, the result of the binary operation:
  • with the & (ampersand token) is the result of the logical AND operation on each pair of the corresponding bits of the input operands.
  • with the | (pipe token) is the result of the logical OR operation on each pair of the corresponding bits of the input operands.
  • with the ^ (hat token) is the result of the logical XOR operation on each pair of the corresponding bits of the input operands.
  • with the << (less than tokens) is the value shifted left with zeros shifted in on the right.
  • with the >> (greater than tokens) is the value shifted right with zeros shifted in on the left.
Left Operand TypeBinary Op(s)Right Operand TypeDescription
intergral & | ^ << >> intergral Returns the result of the bitwise operation as described above. If either operand is not an integral type (bool int32 or int64), the program is ill formed.

Comparisons / Relational

Binary comparison and relational operations compute the result of a equality operand token on two inputs and returns the result. The inputs are not modified, however may be copied and implicitly cast to temporary values if the types do not match. The result type of all comparison operators is of type bool. Binary comparison operations have the following forms:
Operator NameOperator SyntaxReturns
Equal tolhs == rhs Returns true if both operands are equal
Not equal tolhs != rhs Returns true if operands are not equal
Less thanlhs < rhs Returns true the left hand side value is less than the right hand side
Greater thanlhs > rhs Returns true the left hand side value is greater than the right hand side
Less than or equal tolhs <= rhs Returns true the left hand side value is less than or equal to the right hand side
Greater than or equal tolhs >= rhs Returns true the left hand side value is greater than or equal to the right hand side
The following combination of AX type categories are supported for comparison operations (if an operation is not listed, it is not supported):
Left Operand TypeBinary Op(s)Right Operand TypeDescription
scalar== != < > <= >=scalar Returns the result of the scalar comparison.
vector Performs per component comparisons (after implicit conversion) with the lefthand side scalar to every element of the right hand side vector or matrix and perform a logical AND combination on the results of these comparisons. This effectively returns true if every element of the vector or matrix is equal to the scalar.
vec3f a = 2.0f;
int b = 1;
bool c = b == a;
is equal to:
vec3f a = 2.0f;
int b = 1;
bool c = a[0] == b;
for (int i = 1; i < 3; ++i) c &= a[i] == b;
matrix
vector == != < > <= >= scalar Same as scalar op vector
vector Performs binary comparison operations (after implicit conversion) on each pair corresponding components in the vector operands and returns true if all component pairs are equal. Operand sizes must match.
vec3f a = 1, b = 2;
bool c = a == b;
is equal to:
vec3f a = 1, b = 2;
bool c = a[0] == b[0];
for (int i = 1; i < 3; ++i) c &= a[i] == b[i];
matrix == != < > <= >= scalar Same as scalar op matrix
matrix Performs binary comparison operations (after implicit conversion) on each pair corresponding components in the matrix operands and returns true if all component pairs are equal. Operand sizes must match.
mat4f a = 1, b = 2;
bool c = a == b;
is equal to:
mat4f a = 1, b = 2;
bool c = a[0] == b[0];
for (int i = 1; i < 16; ++i) c &= a[i] == b[i];

Logical

Binary logical operations compute and return the result of a boolean operation on two operands. Both operands are implicitly converted to bool types if they are not already.
Warning
These operators are short-circuiting; for logical AND, the second operand is only evaluated if the first is true. For logical OR, the second operand is only evaluated if the first is false. In both cases, the first operand is always evaluated.
They have the following forms:
Operator NameOperator SyntaxReturns
ANDlhs && rhs Returns true if both operands are true. Otherwise, the result is false. This operator is short-circuiting.
Inclusive ORlhs || rhs Returns true if either the first or the second operand is true. This operator is short-circuiting.
The following combination of AX type categories are supported for comparison operations (if an operation is not listed, it is not supported):
Left Operand TypeBinary Op(s)Right Operand TypeDescription
scalar&& ||scalar Returns the result of the scalar logical operation. Both scalars are converted to bools if they are not already.

Unary Operators

Unary operators only execute on a single value. The operator token(s) may come before or after the value, precedence of which is defined by AX's operator precedence. Arithmetic, logical and increment / decrement operators are supported.

Arithmetic

Arithmetic unary operators are comprised of arithemtic and bitwise operators.
Operator NameOperator SyntaxReturns
Unary plus+a Returns the value of its operand, a
Unary minus-a Returns the negative representation of a
Bitwise NOT~a Returns the bitwise NOT (one's complement) value of a. This operator is only valid on integral element types.
The following combination of AX type categories are supported for unary arithmetic operations (if an operation is not listed, it is not supported):
Operand TypeBinary Op(s)Description
scalar+ - ~ Returns the result of the scalar unary operations.
vector Performs per component unary operations, returning a new vector with each element holding the corresponding result. Operand sizes must match.
vec3f a = 2;
vec3f b = -a;
is equal to:
vec3f a = 2;
vec3f b;
for (int i = 0; i < 3; ++i) b[i] = -a[i];
Note: The bitwise not ~ operator is only valid on integer vector types; vec2i, vec3i and vec4i.
matrix+ - Performs per component unary operations, returning a new matrix with each element holding the corresponding result. Operand sizes must match.
vec3f a = 2;
vec3f b = -a;
is equal to:
vec3f a = 2;
vec3f b;
for (int i = 0; i < 3; ++i) b[i] = -a[i];

Logical

Logical unary operators consist of a single operand.
Operator NameOperator SyntaxReturns
Logical NOT!a Returns true if the operand is false. Otherwise, returns false.
The following combination of AX type categories are supported for logical unary operations (if an operation is not listed, it is not supported):
Operand TypeBinary Op(s)Description
scalar! Returns the result of the scalar logical operation. The scalar operand is converted to a bool if it is not already.
vector Performs per component unary operations, returning a new vector with each element holding the corresponding result. Operand sizes must match.
vec3i a = 2;
vec3i b = !a;
is equal to:
vec3i a = 2;
vec3i b;
for (int i = 0; i < 3; ++i) b[i] = !a[i];
Note: The logical not ! operator is only valid on integer vector types; vec2i, vec3i and vec4i.

Increment / Decrement

Increment/decrement operators increment or decrement the value of a scalar, or each component of a vector or matrix. They have the following forms:
Operator NameOperator SyntaxReturns
Pre-increment++a Returns a reference to the incremented result.
Post-incrementa++ Returns a copy of the incremented result.
Pre-decrement--a Returns a reference to the decremented result.
Post-decrementa-- Returns a copy of the decremented result.
Importantly, pre evaluation returns a reference to the value operand, where as post evaluation returns a copy of the operand. The following combination of AX type categories are supported for logical unary operations (if an operation is not listed, it is not supported):
Operand TypeBinary Op(s)Description
scalar ++(pre) (post)++
--(pre) (post)-- 		Returns the result (reference or copy) of the scalar increment or decrement operation.
Note: boolean incrementation and decrementation is not supported. Only int32, int64, float and double types are valid.

Container Access

Container access operators are valid on AX Vector and matrix types. They have the following forms:
Operator NameOperator SyntaxReturns
Dot Component Access vector . component Reference to component component of vector
Container Component Access container [ exp ] Reference to component at index exp of container
Matrix Component Access matrix [ exp1, exp2 ] Reference to component in row exp1, column exp2. Also equal to returning a reference to component at index: [exp1 * dimension + exp2] of matrix where dimension is the the size of the matrix
As data is stored contiguously for both vectors and matrices, the [] operator is valid for both types. However the . operator is only valid on vector types, and the [,] operator is only valid on matrix types. As return values for these operators are references, any modifications through assignments will update the stored value in the container.
. operator
The dot operator . is only valid for vector types. It has the form:
vector . component
Where component is one of the below supported component letters. It only provides access for the first three elements of any vector (for vec2 types, only the first 2 components are accessible). Accessing a vector using the dot operator is fundamentally the same as using the [] operator with the corresponding integer index.
vec4i a = { 6, 7, 8, 9 };
int b = a.z; // get the the third elements value (8)

\[ A=\begin{bmatrix} a_{0}\quad a_{1}\quad a_{2} \end{bmatrix} \]

Component Access Index Result
A.x 0 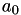$ a_{0} $
A.r 0 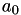$ a_{0} $
A.y 1 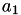$ a_{1} $
A.g 1 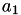$ a_{1} $
A.z 2 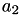$ a_{2} $
A.b 2 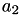$ a_{2} $
This operator can provide more immediately readability when working with expressions that focus on colour or Cartesian coordinate systems.
[] operator
The [] operator is valid for both vectors and matrices. It has the form:
container [exp]
exp is expected to evaluate to a value which is castable to an integer following the assignment casting rules and falls within the valid size of the container. No bounds checking is performed.
As matrices are also an array of contigous values, they can be accessed in the same way. This can make some operations much simplier; a typical example being iterating through all matrix elements and performing some logic:
vec3f a = 0;
a[0] = 1; // valid
a[""] = 1; // invalid - can't cast to int
a[1.2f] = 1; // valid - float exp will be clamped to an int
a[a[0]] = 1; // valid - use the value of a[0] to index into a
// assign each element its actual index value i.e. b[5] = 5;
mat4d b;
for (int i = 0; i < 16; ++i) b[i] = i;
[,] operator
The [,] operator is only valid for matrices. It has the form:
matrix [exp1, exp2]
exp1 and exp2 are expected to evaluate to a value which is castable to an integer following the assignment casting rules and falls within the valid size of the matrix dimensions. No bounds checking is performed. In general it is more readable to use this operator when accessing specific elements, where exp1 is the row index and exp2 is the column index. The tables below show the different access patterns for 3x3 and 4x4 matrices.
mat3f a;
for (int i = 0; i < 3; ++i)
for (int j = 0; j < 3; ++j)
a[i,j] = i*j; // assign matrix element the product of its index

\[ A=\begin{bmatrix} a_{00}\quad a_{01}\quad a_{02}\\ a_{10}\quad a_{11}\quad a_{12}\\ a_{20}\quad a_{21}\quad a_{22}\\ \end{bmatrix} \]

\[ A=\begin{bmatrix} a_{00}\quad a_{01}\quad a_{02}\quad a_{03}\\ a_{10}\quad a_{11}\quad a_{12}\quad a_{13}\\ a_{20}\quad a_{21}\quad a_{22}\quad a_{23}\\ a_{30}\quad a_{31}\quad a_{32}\quad a_{33}\\ \end{bmatrix} \]

Access [a] Access [a,b] Result Access [a] Access [a,b] Result
A[0] A[0,0] 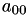$ a_{00} $ A[0] A[0,0] 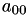$ a_{00} $
A[1] A[0,1] 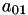$ a_{01} $ A[1] A[0,1] 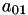$ a_{01} $
A[2] A[0,2] 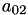$ a_{02} $ A[2] A[0,2] 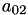$ a_{02} $
A[3] A[1,0] 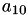$ a_{10} $ A[3] A[0,3] 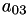$ a_{03} $
A[4] A[1,1] 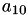$ a_{10} $ A[4] 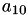A[1,0] $ a_{10} $
A[5] A[1,2] 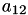$ a_{12} $ A[5] A[1,1] 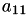$ a_{11} $
A[6] A[2,0] 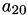$ a_{20} $ A[6] A[1,2] 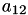$ a_{12} $
A[7] A[2,1] 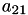$ a_{21} $ A[7] A[1,3] 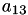$ a_{13} $
A[8] A[2,2] 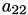$ a_{22} $ A[8] A[2,0] 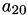$ a_{20} $
A[9] A[2,1] 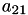$ a_{21} $
A[10] A[2,2] 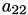$ a_{22} $
A[11] A[2,3] 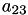$ a_{23} $
A[12] A[3,0] 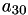$ a_{30} $
A[13] A[3,1] 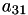$ a_{31} $
A[14] A[3,2] 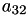$ a_{32} $
A[15] A[3,3] 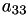$ a_{33} $

Other

A number of uncategorised operators that are more general are documented in this section. They have the following forms:
Operator NameOperator SyntaxReturns
Call / Explicit Cast a(...) Returns the result of a function call or inbuilt explicit cast
Comma a,  b Returns the value of b after chained evaluation
Ternary Conditional a ? b :c b if a is true, c otherwise.
Vector/Matrix Initializer {  a,  b ... } Returns a temporary vector or matrix
Call / Explicit Cast
The function call operator provides the ability to invoke functions or invoke a supported explicit cast. It has the form:
func(a, b, c, ...)
Where func is a function name or a valid explicit cast typename. Explicit casts are only supported for scalar types. For example:
int a = int(1.1f);
vec3f b = 1.0f;
a = int(b.x);
Whilst explicit casts take only a single argument, the operator itself supports multiple or empty arguments for function calls. Whe multiple arguments are provided, they are parsed from first to last and processed in reverse order. However, the order of runtime evaluation is unspecified i.e. they may evaluate in any order. Each function parameter is initialized with its corresponding argument after following implicit conversion of assignments where necessary.
See the function documentation for more information on functions.
Comma
The Comma operator has the form:
a, b
Where a and b are expressions. Chained expressions evaluate each expression in syntactical order (first to last), discarding any return value except for the last expression, which is returned from the entire list. Note that although return values for any expression but the last are discarded, their side effects are still applied before subsequent expression are evaluated. For example:
int a = 5;
a-=1, a+=2; // a = 6
a = a--, ++a; // exp1: a = a--, exp2: ++a. a = 7
Note
Although you may consider the comma operator as a type of binary operator, it is fundamentally different as the types either side of the operator do not interact. Each expression in the comma operator is evaluated independently of all other expressions.
Ternary Conditional
The ternary conditional operator can be thought of as an in-line if-else statement that returns a value, where each of the if/else branches has a single expression that will be returned. It has the form:
a ? b :c
Where a is the condition, evaluated and converted to bool, and b and c are expressions of the same or implicit-castable types. b is evaluated and returned if the condition is true, c is evaluated and returned if the condition is false. Only the expression out of b and c that is returned will be evaluated. Expressions with no return value (a.k.a void) are supported as long as b and c are both of this type.
Also supported is the 'Elvis' operator, a ? : c (or ?:). Here, a is evaluated once, and if when converted to bool is true, a is returned, otherwise c is evaluated and returned. In this case, a and c must be the same or implicit-castable types, and both implicit-castable to bool.
Vector/Matrix Initializer
Vectors and matrices can be represented as local variables (e.g. vec3f), external attributes or parameters (e.g. vec3f@attrib) or as temporary values using the vector/matrix initializer syntax. This operator has the form:
{  a,  b ... }
Where a and b are expressions returning a scalar value. When this operator is invoked with a specific number of arguments, a vector or matrix is implicitly created with a copy of those arguments which can be assigned to an existing container of matching size. Expression in the operator are evaluated from first to last. This operator is only valid with argument lists of sizes 2, 3, 4, 9 and 16, which implicitly represent vec2, vec3, vec4, mat3, and mat4 types respectively. For example:
vec3f a = { 1.0f, 2.0f, 3.0f }; // right hand side of assignment creates a vec3f
vec3f b = dot(a, { a[0], 5.0, 6.0 }); // second argument creates a vec3d
Note
In the above examples, the value of a[0] is copied into the initializer operator.
Initialization Type
A mixture of arbitrary scalar types can be used in the initializer operator e.g:
mat3f a = {
true, 0s, 0,
0l, 0.0f, 0.0,
false, 1, 2
};
The temporary container evaluates all expressions and uses the highest ranking type (as defined by arithmetic type precedence) to infer the element type of the container, implicitly casting all other types to that type where necessary. In the above example, the temporary created forms a mat3d, before being implicitly cast to a mat3f due to the assignment.

Operator Precedence

The below table shows the precedence and associativity of all AX operators. Operators are listed in descending precedence.
Precedence Operator Description Associativity
1 () Parenthesis Left-to-right
2 a++ a-- Suffix/postfix Increment / Decrement
type() Functional cast
a() Function call
a[] . Container Access
3 ++a --a Prefix Increment / Decrement Right-to-left
+a -a Unary plus and minus
! ~ Logical NOT and Logical NOT
4 a*b a/b ab Multiplication, division, and remainder Left-to-right
5 a+b a−b Addition and subtraction
6 << >> Bitwise left shift and right shift
7 < <= For Comparisons / Relational operators < and ≤ respectively
> >= For Comparisons / Relational operators > and ≥ respectively
8 == != For Comparisons / Relational operators = and ≠ respectively
9 & Arithmetic AND
10 ^ Arithmetic XOR (exclusive or)
11 | Arithmetic OR (inclusive or)
12 && Logical AND
13 || Logical OR
14 a?b:c Ternary operator Right-to-left
= Direct assignment
+= -= Compound assignment by sum and difference
*= /= %= Compound assignment by product, quotient, and remainder
<<= >>= Compound assignment by bitwise left shift and right shift
&= ^= |= Compound assignment by bitwise AND, XOR, and OR
15 , Comma Left-to-right
Note that associativity of unary operators is redundant (unary prefix operators are always right-to-left and unary postfix operators are always left-to-right). Operators that have the same precedence are bound to their arguments in the direction of their associativity. For example, the expression a = b = c is parsed as a = (b = c), and not as (a = b) = c because of right-to-left associativity of assignment, but a + b − c is parsed (a + b) − c and not a + (b − c) because of left-to-right associativity of addition and subtraction. Note that this is based off the C++ operator precedence.

Tokens

Variable Identifiers

Literals

Literals can be thought of as constant values that are known at compile time. e.g.
i@a = 1; // the number 1 is a literal
As AX supports different bit width scalar literals, it also supports suffix literal tokens which, when using with a scalar literal, represent a literal of a specific size. AX also supports implicit casting for all assignment and arithmetic operations, so any literal can be used to assign any scalar a value.
TypeLiteral Tokens
boolTokens true and false
int32No suffix, automatically infered from integral literals
int64The letter l e.g.
int64 a = 10l;
floatThe letter f e.g.
float a = 0.0f;
doubleNo suffix, automatically infered from floating point literals.
stringCharacter strings wrapped in double quotes " "

Comments

Keywords

Reserved Keywords


Syntax

Attribute Access

float@surface = float@density;
Assignment operations determine which volumes will be executed over. Here, the AX program will only execute on the surface VDB whilst retaining access to all available VDBs. There exists a number of possible states of both the surface and density volumes.
  • Volumes have the same transform and the same topology
  • Volumes have the same transform, but different topologies
  • Volumes have different transforms, but the same topology
  • Volumes have different transforms and different topologies
Matching Transforms
In the simplest case, all volumes processed have the same transform. Active voxels in the surface VDB will receive a value sampled (point sampled) at the corresponding index space position in the density VDB. As the transforms match, this is guaranteed to be at the same world space position. The topology of the density VDB does not influence which values are assigned, AX simply queries the density VDB at the computed position and uses whatever value is returned. This may be the VDB Background value.
Different Transforms
When transforms differ, AX performs coordinate transformations from the source VDB to the target VDB. Using some simple pseudo code, we can represent each voxel's coordinate query:
1 foreach(ActiveVoxel in surface)
2  SurfaceIndexSpaceCoord = ActiveVoxel.indexSpaceCoordinate();
3  SurfaceWorldSpaceCoord = surface.transformToWorld(SurfaceIndexSpaceCoord);
4  DensityIndexSpaceCoord = density.transformToIndex(SurfaceWorldSpaceCoord);
5  ActiveVoxel = density.getValue(DensityIndexSpaceCoord);
done() –>

External Parameter Access

Declarations

Scopes

Branching (if / else)

Loops


Functions

For a list of all functions, see the AX Function List.
AX supports a variety of mathematical, string, utility and custom function calls which can be used from within an AX program. Native function support is constantly growing and we encourage users who wish to see particular methods exposed and supported natively by AX to contact us. Whilst we can't guarantee to accommodate every function, these requests provide the developers insights into how the language is being used.
Function Execution Context
Some functions depend on the currently processing OpenVDB Execution Context to work correctly and will fail if called from an "invalid" context. Specifically, there exists functions which operate on OpenVDB points or OpenVDB volume grids and interact with the point or voxel data. Some of these methods are incompatible for the other grid type (for example, deleting a point from a Point Data Grid) and will result in the compilation failure of an AX program if an attempt is made it use them.

User Functions

User function declarations are not currently supported, but exist on the AX Roadmap as a near future feature.

AX VEX Support

Generated by   doxygen 1.8.11